NMR Theory Hopefully Explained
NMR, nuclear magnetic resonance, is important because it provides a powerful way to deduce the structures of organic molecules. In addition, the same principle is used in MRI medical imaging. Unfortunately, the physics behind NMR is extremely complicated. What follows is an attempt to provide all the information you need to understand the basic principles underlying the NMR technique.
1.0 Moving charge-magnetic field interactions:1.1 Moving charges (electrons, protons) create a magnetic field.
1.2 Charges will interact with an external magnetic field (created by a big magnet in the laboratory), causing them to move in response to the field. This, in turn, induces an additional magnetic field because of 1.1.
1.3 This is how electromagnets and other cool things like generators work, but also describes how charged subatomic particles, namely electrons and protons in molecules, interact with a magnetic field and also how they interact with each other.
2.0 Quantum mechanical description of nuclear spin. These are the essential facts you need before we describe NMR.
2.1 Atomic nuclei with an odd atomic mass or an odd atomic number have a quantum mechanical property called “spin” that is designated by a spin quantum number such as 1/2 or 1. For NMR experiments, we are only concerned with nuclei having a spin quantum number of 1/2. In particular we are interested in 1H (most common isotope of hydrogen by far) and 13C (rare but useful isotope of carbon, the most common isotope being 12C). Recall from general chemistry that the number 1,12, 13 etc. is the atomic mass, that is, the total number of protons and neutrons in the given isotope.
2.2 Nuclear spin can be thought of as the positive charge of protons “circulating”. In other words you should think about nuclear spin as circulating charge. I know this sounds weird, but just accept it and realize this is best way to think about spin. There are two consequences here:
2.2A Nuclear spin can interact with an external magnetic field.
2.2 B Nuclear spin creates its own magnetic field that can interact with other nuclei having spin.
2.3 Nuclei with spin can have only a fixed number of allowed states (i.e. the number of states are quantized, hence the term "quantum" mechanics).
2.3A Nuclei with spin quantum number of 1/2 have two allowed spin states, +1/2 and –1/2. “Allowed” is a fancy way of saying this is what can happen. In other words, any given nucleus will either be in a spin state of +1/2 or –1/2.
2.3B In the absence an external magnetic field, nuclei in either a +1/2 or –1/2 spin state are of the same energy.
2.3C The key idea for the NMR experiment is that in an external magnetic field, the two spin states have different energies. The +1/2 spin state is lower in energy, and the –1/2 spin state is higher in energy. The difference in energy is directly proportional to the strength of the external magnetic field. In other words, the bigger the magnet in the laboratory, the larger the difference in energy between +1/2 and –1/2 nuclear spin states.
Now, review the above so you can recite all of the points. These form the basis of the NMR experiment. Sorry about the complicated story here, but this is important for another reason. It answers the question “How does MRI work?”, a question many of you will be asked when you become physicians.
3.0 The NMR experiment
3.1 The simplest NMR experiment is carried out such that a sample is placed in a strong, constant magnetic field. The sample is irradiated with electromagnetic radiation. When the energy of the electromagnetic radiation corresponds exactly to the difference in energy between the +1/2 and -1/2 spin states, the sample absorbs the energy as nuclear spins are excited from the lower energy spin state (+1/2) to the higher energy spin state (-1/2). The process of having the nuclear spin change from +1/2 to -1/2 through absorption of energy is called resonance (hence the "R" in NMR).3.1A. Following excitation of the nucleus from the +1/2 to the -1/2 spin states, the nucleus will relax back to the +1/2 spin state, a process that emits electromagnetic radiation of the same frequency that was absorbed.
3.1B. The NMR spectrometer measures the exact frequency of the energy that is absorbed.
3.1C The electromagnetic radiation used is in the radio frequency range.
3.1D The NMR spectrometer consists of a strong magnet in which the sample is placed. The sample is usually dissolved in solvent, then placed in a tube that is spun in the magnet. A radiofrequency generator excites the sample, and sensitive electronics detect when the energy is absorbed.
3.1E Modern NMR spectrometers operate using the principle of Fourier transform, the details of which are probably beyond the scope of this class. I just wanted you to know this was out there, but we will not be discussing it much detail because it requires an explanation of much more complex quantum mechanics.
4.0 Information obtained from and NMR spectrum
4.1 If all nuclei in a molecule absorbed the same frequency of electromagnetic radiation, the NMR experiment would not be useful.
4.2 In fact, different nuclei absorb radio frequency electromagnetic radiation at slightly different characteristic frequencies, and because of this you can determine which types of atoms are present in a molecule. More importantly, adjacent atoms with spin influence the frequency as well, so you can tell which atoms are adjacent to each other in a molecule. In other words, you can determine what functional groups are present and how they are connected to each other, i.e. the structure of an organic molecule, with NMR!
5.0 More physics.
5.1 Both electrons and other nuclei with spin in a molecule have their own magnetic fields.
5.2 The magnetic field “felt” by any given nucleus in a molecule is actually the sum of (i) the external magnetic field plus (ii) the magnetic field of the electrons around the nucleus plus (iii) the magnetic fields caused by the different spin states of adjacent nuclei.
5.2A Electron density around a nucleus circulates in a characteristic fashion when placed in the magnetic field. (See 1.2 above). This circulation creates its own magnetic field that opposes the external magnetic field (See 1.1 above). Thus, nuclei surrounded by more electron density are more shielded from the external magnetic field and these nuclei “feel” a smaller total magnetic field. Nuclei surrounded by less election density are less shielded. Read these sentences again as they are key to understanding NMR, and this concept is really subtle.
5.2B The magnetic field produced by a nucleus in a –1/2 spin state is different than the magnetic field produced by a nucleus in a +1/2 spin state. At room temperature, any given nucleus in a magnetic field has only a slight excess of probability of being in the lower energy state. Thus, across a population of molecules in a sample, it is roughly 50-50 whether a given nucleus is in the +1/2 or –1/2 spin state. Thus, over a population of molecules in a sample, for a given atom X that is adjacent to another atom Y: around half of the molecules will have X experiencing the magnetic field from a +1/2 spin state of the Y nucleus, and the other half of molecules will have X experiencing the magnetic field from a -1/2 spin state of the Y nucleus. Similarly, around half of the molecules will have Y experiencing the magnetic field from a +1/2 spin state of the X nucleus, and the other half of molecules will have Y experiencing the magnetic field from a -1/2 spin state of the X nucleus.The importance of 5.2A and 5.2B cannot be overstated. These are the keys to interpreting NMR spectra. Make sure you understand them before going on!
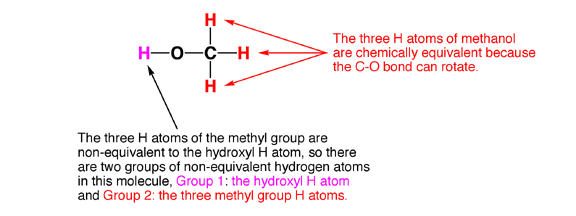
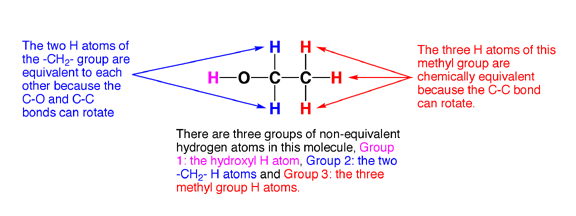
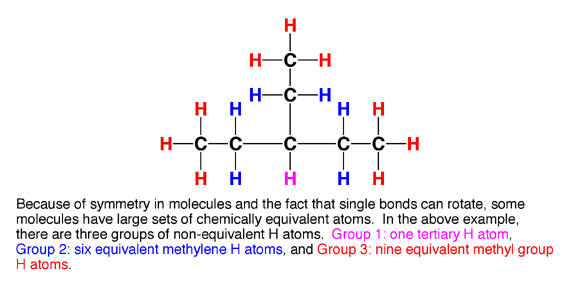
6.0 Chemical equivalence. Here is the last piece of the puzzle. Certain atoms in a molecule are equivalent. Trust me this is important and it is key to the NMR story.
6.1 Chemically equivalent atoms are atoms in a molecule that have the same chemical environment. That is, they have the same electron density, and the same distance and connectivity relationship to all the other atoms in the molecule. This is possible largely because single bonds such as C-C bonds rotate freely at room temperature, so H atoms connected to the same rotating C atom will on average all see the same chemical environment as they rotate around (unless they are adjacent to a chiral center, but that is another story). The following examples illustrate how to identify groups of equivalent H atoms in molecules.